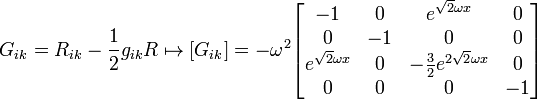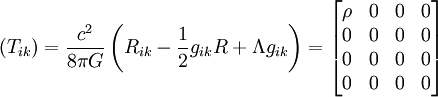Gödel universe

Metrical form of the Gödel universe

The geometry of the Gödel universe is represented in a spacetime where metrics can be represented by means of coordinates pseudocartesianas and units that = 1 in such a way:

Where It is a constant, associated to the vorticity of the flow of matter, also this vorticity can relate with the density of matter in the universe, as explained in the section on the material content.

General properties of the Gödel spacetime

The Gödel universe is a solution of Einstein's equations with cosmological constant full of powdery material, i.e. without pressure . The gravitational Einstein tensor given by is:

It is easy to see that if a value of the cosmological constant that meets is taken:

Then the energy-boosting tensor is given in coordinates (t, x, y and z):

The Gödel universe and the possibility of time travel

An interesting mathematical property of the Gödel universe, is that around every point there are curves temporary closed, which physically is that an observer can travel into the future and reach a point in their past, cyclically repeating this movement. This property suggests that this solution is physically unrealistic or impossible. The surprising thing about the Gödel solution is that the universe is composed of matter not exotic convecional despite this unusual property and that if it were possible to give this motion of vorticity which implies the equation we would have a universe with this strange causal property.